Answer:
-1/5
Explanation:
What are parallel lines?
Lines that are parallel never touch. They can extend infinitely and they will still never touch. In order for this to happen the slope of the two lines must be the same. So if we want to find the slope of every line that is parallel to the line on the graph, we simply find the slope of the line of the graph.
Finding the slope
We can find the slope using the following formula:
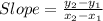
Where the x and y values are derived from any given points on the line (x1,y1) and (x2,y2)
Here the given points are (-5,-1) and (0,-2)
So we have (x1,y1) = (-5,-1) meaning x1 = -5 and y1 = -1
We also have (x2,y2) = (0,-2) meaning x2 = 0 and y2 = -2
Now we plug these values into the formula
Recall formula :
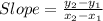
==> Plug in x1 = -5 , y1 = -1 , x2 = 0 and y2 = -2

==> simplify numerator and denominator

So the slope of the line is -1/5
This means the slope of any parallel line to that line would also have a slope of -1/5