Question

the graph below represents the liner equation y equals 1 and 1/2 x -3 A second linear equation is represented by data in the table. What is the solution to the system of equations​

Answer 1

C. (2, -2)

Step-by-step explanation:

Given:

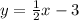`y = (1)/(2)x - 3` ----› Equation 1

Use the table to generate equation two of the system.

First, find the slope (m), and y-intercept (b).

Using two pairs, (0, 0) and (2, -2),

`slope (m) = (y_2 - y_1)/(x_2 - x_1) = (-2 - 0)/(2 - 0) = (-2)/(2) = -1`

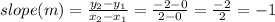
y-intercept (b) = 0 (i.e the value of y when x = 0)

Substitute m = -1, and b = 0 in
`y = mx + b`

Thus:

`y = (-1)(x) + 0`

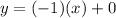
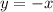`y = -x` ----› Equation 2.

✔️Solve for x by substituting y = -x in equation 1

`y = (1)/(2)x - 3`

`-x = (1)/(2)x - 3`

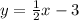
Add 3 to both sides

`-x + 3 = (1)/(2)x - 3 + 3`

`-x + 3 = (1)/(2)x`

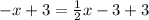
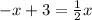
Multiply both sides by 2

`(-x + 3) * 2 = (1)/(2)x * 2`

`-2x + 6 = x`

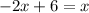
Collect like terms

`-2x - x = -6`

`-3x = -6`

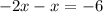
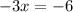
Divide both sides by -3

`x = 2`

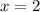
✔️Substitute x = 2 in equation 2.

`y = -x`

`y = -2`

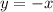
Therefore the solution to the system of equations would be:

(2, -2)