Answer:
the rate charged per hour by the first mechanic is 75 $/hr and the rate charged per hour by the second mechanic is 100 $/hr.
Explanation:
A system of equations is a set of two or more equations in various unknowns in which you want to find a common solution.
So, first of all it is convenient to define the system variables:
- x= the rate charged per hour by the first mechanic
- y= the rate charged per hour by the second mechanic
If the sum of the two rates were $ 175 per hour, then the mathematical expression that represents this situation is: x + y= 175
You know that the first mechanic worked for 20 hours, and the second mechanic worked for 15 hours. Then the amount of money won by the first and second mechanic respectively is expressed by 20*x and 15*y. Together they charged a total of $3000, then 20*x + 15*y=3000
So, the system of equations to solve is:
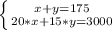
Solving a system of equations consists of finding the value of each unknown so that all the equations of the system are satisfied.
There are several methods for solving a system of equations. One of them is the substitution method, which consists of solving or isolating one of the unknowns (for example, x) and substituting its expression in the other equation. In this way, you obtain an equation of the first degree with the other unknown. Once solved, you must calculate the value of x by substituting the already known value of y.
In this case, you isolate the variable x from the first expression:
x= 175 - y
Replacing this expression in the second equation:
20*(175 - y)+15*y=3000
and solving you get:
20*175 -20*y +15*y=3000
3500 -20*y +15*y=3000
3500 -5*y=3000
-5*y=3000 -3500
-5*y= -500
y= (-500)÷(-5)
y= 100
So:
x=175 -y
x=175 -100
x=75
Then the rate charged per hour by the first mechanic is 75 $/hr and the rate charged per hour by the second mechanic is 100 $/hr.