
★ Curved surface area of right circular cylinder is 4.4 m².
★ Radius of base of the cylinder is 0.7 m.
★
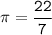

★ The height of cylinder.

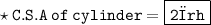

Let,
❍ The height of circular cylinder be
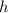
❍ Radius [r] of base of cylinder be 0.7 m
We know,
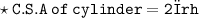
Putting,
☆
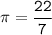
☆ r as 0.7
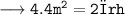
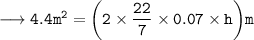
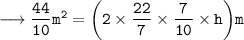
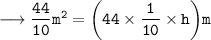
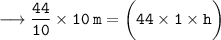
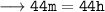
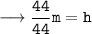
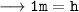
Therefore, the height of cylinder = 1 m.
