Question

The value of a rare baseball card issued in 1989 is represented by the function )-0.2-252+3x +4 where x represents the number of years since the baseball card was issued. Use the Remainder Theorem to find the value of the card in 1999

Answer 1

The correct format of the question is

The value of a rare baseball card issued in 1989 is represented by the function f(x) =
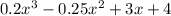`0.2x^3- 0.25x^2+3x +4` where x represents the number of years since the baseball card was issued. Use the Remainder Theorem to find the value of the card in 1999

Answer:

The value of the card in 1999 is 209

Explanation:

The remainder theorem says that

If you divide a Polynomial by f(x) be a Linear factor of the form (x-a) the remainder will be equal to F(a).

f(x) =
`0.2x^3- 0.25x^2+3x +4`

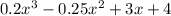
So we need to find from 1989 to 1999 which is 10 years

so our a = 10

Factor will be x-10

Applying remainder theorem

`( 0.2x^3 -0.25x^2+3x+4)/(x-10)`

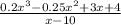
we will get

Quotient =
`0.2x^2 + 1.75x +20.5`

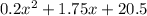
Remainder = 209

Verifying our result

F(10) =
`0.2(10)^3 -0.25(10)^2 + 3(10) + 4`

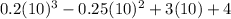
= 200 -25 + 30 + 4

= 209