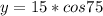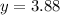Question

When Carla solved for the height from the ground to the point where the ladder

touches the wall, she used the 75 degree angle. Explain how Carla solved for the
distance to the top of the ladder. Find the distance, rounding your answer to the
nearest tenth of a foot. *

Answer 1

See explanation

Step-by-step explanation:

Given

Represent the vertical angle with
`\theta`

`\theta = 75`

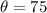
The question has incomplete details because the length of the ladder is not given; neither is the distance between the ladder and the wall given.

See attachment for illustration

So, this solution will be based on assumptions.

Represent

- The height from ground to the top of the ladder with y

- The length of the ladder with L

- The distance between the ladder and the wall with x

Carla could solve for y in any of the following ways:

1. Tan formula

`tan \theta = (opp)/(adj)`

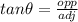
In this case:

`tan \theta = (x)/(y)`

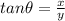
Multiply both sides by y

`y * tan \theta = (x)/(y) * y`

`y * tan \theta = x`

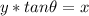
Divide both sides by tan

`y = (x)/(tan \theta)`

`y = (x)/(tan 75)`

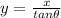
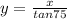
This can be used if the distance (x) between the ladder and the wall is known.

Assume x = 15

`y = (15)/(tan 75)`

`y = 4.02`

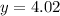
2. Cosine formula

`cos \theta = (adj)/(hyp)`

In this case:

`cos \theta = (y)/(L)`

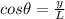
Multiply both sides by L

`L * cos \theta = (y)/(L) * L`

`Lcos \theta = y`

`y = Lcos \theta`

`y = Lcos75`

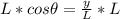
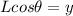
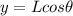
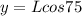
This can be used if the length (L) of the ladder is known.

Assume L = 15

`y = 15 * cos75`

`y = 3.88`