Question

The number of responses to a survey are shown in the Pareto chart. The survey asked 1052 adults how they would grade the quality of their public schools. Each person gave one response,

Find each probability

(a) Randomly selecting a person from the sample who did not give the public schools an A

(1) Randomly selecting a person from the sample who gave the public schools a grade better than a D

(c) Randomly selecting a person from the sample who gave the public schools a Dor an F

(d) Randomly selecting a person from the sample who gave the public schools an A or B

(a) The probability that a randomly selected person did not give the public schools an Als

(Round to three decimal places as needed)

Answer 1

Answer: (a) P(no A) = 0.935

(b) P(A and B and C) = 0.0005

(c) P(D or F) = 0.379

(d) P(A or B) = 0.31

Explanation: Pareto Chart demonstrates a relationship between two quantities, in a way that a relative change in one results in a change in the other.

The Pareto chart below shows the number of people and which category they qualified each public school.

(a) The probability of a person not giving an A is the difference between total probability (1) and probability of giving an A:

P(no A) =
`1-(68)/(1052)`

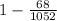
P(no A) = 1 - 0.065

P(no A) = 0.935

b) Probability of a grade better than D, is the product of the probabilities of an A, an B and an C:

P(A and B and C) =
`((68)/(1052))((258)/(1052))((327)/(1052))`

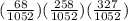
P(A and B and C) =
`(5736888)/(1164252608)`

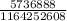
P(A and B and C) = 0.0005

c) Probability of an D or an F is the sum of probabilities of an D and of an F:

P(D or F) =
`(269)/(1052) +(130)/(1052)`

P(D or F) =
`(399)/(1052)`

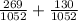
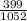
P(D or F) = 0.379

d) Probability of an A or B is also the sum of probabilities of an A and of an B:

P(A or B) =
`(68)/(1052) +(258)/(1052)`

P(A or B) =
`(326)/(1052)`

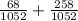
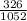
P(A or B) = 0.31