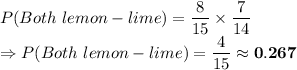Question

Find the probability. A cooler contains fifteen bottles of sports drink: seven lemon-lime flavored and eight orange flavored. You randomly grab a bottle and give it to your friend. Then, you randomly grab a bottle for yourself. You and your friend both get lemon-lime. 3 13 ≈ 0.231 4 9 ≈ 0.444 1 5 = 0.2 4 15 ≈ 0.267

Answer 1

`(4)/(15) \approx \bold{0.267}`

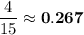
Explanation:

Given that:

Number of lemon - lime flavored bottles = 8

Number of orange flavored bottles = 7

Bottles are picked one by one.

First for the friend and then for the person himself.

To find:

The probability that both the bottles drawn are of lemon-lime flavor.

Solution:

Total number of bottles available in the cooler = 8 + 7 = 15

Formula for probability of an event E can be observed as:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

`P(First\ lemon-lime) = (8)/(15)`

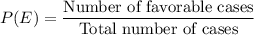
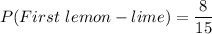
Now, lemon - lime flavored bottles left = 7

Total number of bottles left = 14

`P(Second\ lemon-lime)=(7)/(14)`

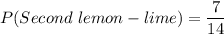
Required probability:

`P(Both\ lemon - lime) = (8)/(15)* (7)/(14)\\\Rightarrow P(Both\ lemon - lime) = (4)/(15) \approx \bold{0.267}`