Question

Three pipes A, B and C take 24, 36 and 32 hours to fill a pool, respectively. How long would it take the three pipes to fill the pool if pipe B is turned on 3 hours after pipe A and pipe C is turned on 1 hour after pipe B?

Answer 1

12 hours

Explanation:

Time taken by pipe A = 24 hours

Time taken by pipe B = 36 hours

Time taken by pipe C = 32 hours

To find:

How long would it take the three pipes to fill the pool if pipe B is turned on 3 hours after pipe A and pipe C is turned on 1 hour after pipe B?

Solution:

First of all, let us assume the total capacity of the pool.

Let us take LCM of 24, 36 and 32.

LCM of 24, 36 and 32 = 288

Let the total capacity of the pool = 288 units

Total units filled by pipe A in one hour =
`(288)/(24) = 12\ units`

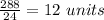
Total units filled by pipe B in one hour =
`(288)/(36) = 8\ units`

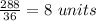
Total units filled by pipe C in one hour =
`(288)/(32) = 9\ units`

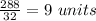
Now, for the first 3 hours, only pipe A operates, so units filled in first three hours =
`12* 3 =36\ units`

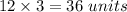
For the next one hour, A and B both operate together, so units filled in the next 1 hour = 12 + 8 = 20 units

Total number of units filled in 4 hours = 36 + 20 = 56 units

Units to be filled to completely fill the pool = 288 - 56 = 232 units

Now, after the 4th hours, all the pipes operate together.

So, number of units filled in each hour = 12 + 8 + 9 = 29 units

Time taken to fill 232 units =
`(232)/(29) = 8\ hours`

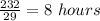
Total time taken = 4 + 8 = 12 hours