Answer:
The amounts invested in the account = ¢ 18000
and the amount invested in the stock = ¢40000-¢18000= ¢22000.
Explanation:
Given that the account paying 4% interest and the stocks paying 6% interest.
Assuming she put ¢ x in the account, so
Income (interest) from the account = 4% of x = ¢ 0.04x...(i)
She has a total of ¢ 40000 to invest, so the remaining amount = ¢(40000-x).
As she put the remaining amount into stock, so
Income (interest) from the stock=6% of (40000-x)=¢(2400-0.06x)...(ii)
As total income from the investment is ¢ 2040, so on adding both the incomes from equations (i) and (ii), we have
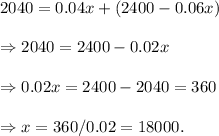
So, the amount invested in the account = ¢ 18000
and the amount invested in the stock = ¢40000-¢18000= ¢22000.