Question

In a liquid metal fast breeder reactor, no neutron moderation is desired and sodium is used as a coolant to minimize fission-neutron thermalization. How many elastic scatters with sodium, on the average, would it take for 2-MeV neutrons to reach an average thermal energy of 0.025 eV?

Answer 1

219 scatterings

Step-by-step explanation:

Given that:

The Coolant used In the liquid metal fast breed reactor = Sodium

The atomic weight (A) of sodium = 23

The initial energy
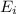`E_(i)` = 2 - MeV

The final energy
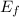`E_(f)` = 0.025 eV (thermal energy)

The number of elastic neutron scatterings (n) needed to reach the given average thermal energy can be computed as:

`n = (log \bigg((E_f)/(E_i) \bigg))/(log \bigg [ (A^2+1)/((A+1)^2) \bigg])`

`n = (log \bigg((0.025)/(2 * 10^6) \bigg))/(log \bigg [ (23^2+1)/((23+1)^2) \bigg])`

`n = (log \bigg(1.25* 10^(-8) \bigg))/(log \bigg [ 0.92014\bigg])`

`n = 218.643`

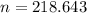
n ≅ 219 scatterings