Question

The arithmetic sequence a_ia i ​ a, start subscript, i, end subscript is defined by the formula: a_1 = 15a 1 ​ =15a, start subscript, 1, end subscript, equals, 15 a_i = a_{i - 1} -7a i ​ =a i−1 ​ −7a, start subscript, i, end subscript, equals, a, start subscript, i, minus, 1, end subscript, minus, 7 Find the sum of the first 660660660 terms in the sequence.

Answer 1

-1,512,390

Explanation:

Given

a1 = 15

`a_i = a_(i-1) -7`

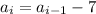
Let us generate the first three terms of the sequence

`a_2 = a_(2-1)-7\\a_2 = a_1 - 7\\a_2 = 15-7\\a_2 = 8`

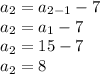
For
`a_3`

`a_3 = a_(3-1)-7\\a_3 = a_2 - 7\\a_3 = 8-7\\a_3 = 1`

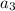
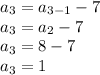
Hence the first three terms ae 15, 8, 1...

This sequence forms an arithmetic progression with;

first term a = 15

common difference d = 8 - 15 = - -8 = -7

n is the number of terms = 660 (since we are looking for the sum of the first 660 terms)

Using the formula;

`S_n = (n)/(2)[2a + (n-1)d]\\`

Substitute the given values;

`S_(660) = (660)/(2)[2(15) + (660-1)(-7)]\\S_(660) = 330[30 + (659)(-7)]\\S_(660) = 330[30 -4613]\\S_(660) = 330[-4583]\\S_(660) = -1,512,390`

Hence the sum of the first 660 terms of the sequence is -1,512,390