Answer:
h = 8.845 m
Explanation:
The height h(t) of the football above the ground in meters t seconds after being punted is affected by gravity and by the punters kick, and can be represented as the difference of two functions:
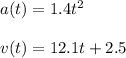
We need to find h(t) such that, h(t)=v(t)-a(t)
So,

It is a quadratic equation. When we solve it we get :
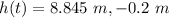
Neglecting negative value,
h(t) = 8.845 m
So, the ball was at a height of 8.845 m when it was punted.