Question

Which geometric series converges?

Answer 1

Option (1)

Explanation:

In a geometric series,

`\sum_(n=0)^(\infty)ar^n=a+ar^1+ar^2+....`

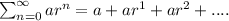
Here r =
`(a_n)/(a_(n-1))`

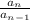
For |r| < 1, series will converge.

For |r| > 1, series will diverge.

Option (1)

Given geometric series is,

`(1)/(2)+(1)/(4)+ (1)/(8)+ (1)/(16).......`

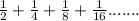
Common ratio =
`((1)/(4))/((1)/(2) )`

=
`(1)/(2)`

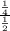
Since,
`(1)/(2)<1`

Series will converge.

Option (2)

`(1)/(2)+1+2+4+......`

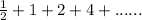
r =
`(1)/((1)/(2))=2`

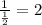
Since, 2 > 1,

Series will diverge.

Option (3)

`(1)/(2)+ (3)/(2)+ (9)/(2)+ (27)/(2)+......`

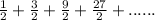
Common ratio 'r' =
`((3)/(2) )/((1)/(2) )=3`

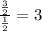
Since, 3 > 1,

Series will diverge.

Option (4)

`(1)/(2)+3+18+108+.....`

Common ratio 'r' =
`(3)/((1)/(2))=6`

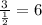
Since, 6 > 1

Series will diverge.

Therefore, Option (1) will be the correct option.