Answer:
PQ is 10.
QR is 5.
Hence, PQ=2QR
Explanation:
We have the three points P(-1, 3); Q(7, -3); and R(4, 1).
And we want to show that PQ=2QR.
In other words, we want to show that PQ/QR=2.
So, let's find PQ and QR. We will need to use the distance formula:
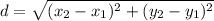
To find PQ:
P is (-1, 3) and Q is (7, -3).
So, we will let P(-1, 3) be (x₁, y₁) and Q(7, -3) be (x₂, y₂).
Substitute the values into the distance formula. This yields:

Evaluate:

Evaluate:
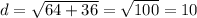
So, the distance of PQ is 10.
And to find QR:
Q is (7, -3) and R is (4, 1).
Again, we will let Q(7, -3) be (x₁, y₁) and R(4, 1) be (x₂, y₂).
Substitute appropriately. So:
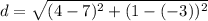
Evaluate:
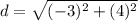
Evaluate:
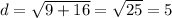
So, the distance of QR is 5.
Therefore, it follows that:

And we have shown that PQ=2QR.