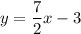Answer:
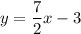
Explanation:
We wan to determine the equation of a line that passes through the point (2, 4) and is parallel to:
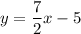
Since our new line is parallel to our equation, this means that the two lines have the same slope.
Therefore, the slope of our new line is also 7/2, the slope of the original.
Now, we can use the point-slope form:
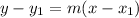
Where m is the slope and (x₁, y₁) is a point.
So, we will substitute 7/2 for m.
Let's let our point (2, 4) be (x₁, y₁). Hence:
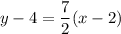
Solve for y. Distribute:
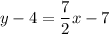
Add 4 to both sides.Therefore, our equation is: