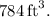Final Answer:
The volume of the pyramid with an edge length of 14 ft and a height of 12 ft is approximately 784 cubic feet.
Explanation:
The formula for the volume of a pyramid is given by:
![\[ V = (1)/(3) * \text{base area} * \text{height} \]](https://img.qammunity.org/2021/formulas/mathematics/college/gqkx3vitp2b7yl0f2isodhl3bf10cxqlnc.png)
In this case, the pyramid has a square base, so the base area is
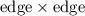 . The given values are:
. The given values are:
![\[ \text{edge} = 14 \, \text{ft} \]](https://img.qammunity.org/2021/formulas/mathematics/college/j7h1eszzijk89prxwx18ze8muj88dunfc8.png)
![\[ \text{height} = 12 \, \text{ft} \]](https://img.qammunity.org/2021/formulas/mathematics/college/r3xgn00vy4vjt09wi1nbi8u3ab13lnqe9v.png)
Let's substitute these values into the formula and calculate the volume:
![\[ \text{base area} = \text{edge} * \text{edge} = 14 \, \text{ft} * 14 \, \text{ft} \]](https://img.qammunity.org/2021/formulas/mathematics/college/qmb5pz4xrabtz9n82xcblgbpseo4qpnche.png)
![\[ \text{base area} = 196 \, \text{ft}^2 \]](https://img.qammunity.org/2021/formulas/mathematics/college/wq5z7c0ic6jprk3l2dghrl1g9akahgtzn9.png)
Now, substitute the values into the volume formula:
![\[ V = (1)/(3) * 196 \, \text{ft}^2 * 12 \, \text{ft} \]](https://img.qammunity.org/2021/formulas/mathematics/college/ivfk9c1dlgvyns0qmt9tleiatqtjek8pog.png)
![\[ V = (1)/(3) * 2352 \, \text{ft}^3 \]](https://img.qammunity.org/2021/formulas/mathematics/college/bm2i8y1xmhp26pzyg2uzlk0vc2ykk67dd9.png)
![\[ V \approx 784 \, \text{ft}^3 \]](https://img.qammunity.org/2021/formulas/mathematics/college/i0qu1xai8z5j97bjpjj4ywfl6b7lb4cs6h.png)
Therefore, the volume of the pyramid is approximately