Answer:
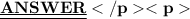
Let the speed of the train be x km/hr and the speed of the bus is y km/hr.
So according to question and using

Total distance =300 km
Mansi travels 60 km by train and 300−60=240 by bus in 4 minute,

and 100 km by train, 300−100=200 by bus, and takes 10 minutes more,
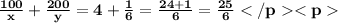
Now, let
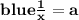
and.
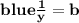
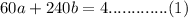
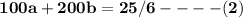
multiply (1) by 5 and (2) by 6 we get
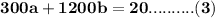
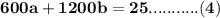
Subtracting (3) and (4) we get
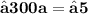

Putting the value of a in (1) we get
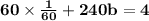
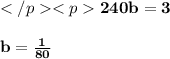
Now ,


Hence, the speed of the train is 60 km/hr and the speed of the bus is 80 km/hr.