Answer:
The correct answer is: "Option [D]".
Explanation:
Hi student, let me help you out!
....................................................................................................................................
Let's use the acronym PEMDAS. With the help of this little acronym, we will not make mistakes in the Order of Operations! :)

P=Parentheses,
E=Exponents,
M=Multiplication,
D=Division,
A=Addition,
S=Subtraction.
Now let's start evaluating our expression, which is
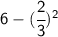
According to PEMDAS, the operation that we should perform is "E-Exponents".
Notice that we have a fraction raised to a power. When this happens, we raise both the numerator (2 in this case) and the denominator (3 in this case) to that power, which is 2. After this we obtain
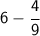 .
.
See, we raised both the numerator and the denominator to the power of 2.
Now what we should do is subtract fractions.
Note that 6 and -4/9 have unlike denominators. First, let's write 6 as a fraction:
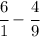 . Now let's multiply the denominator and the numerator of the first fraction times 9:
. Now let's multiply the denominator and the numerator of the first fraction times 9:
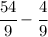 .
.
See, now the fractions have the same denominator. All we should do now is subtract the numerators:
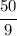 .
.
∴, the answer is Option D.
Hope this helped you out, ask in comments if any queries arise.
Best Wishes!

