Question

In in the previous activity you solved a system of equations representing the carnival admissions using the elimination method in this activity you will solve the same system using substitution then you'll compare your solution with the solution you obtained in the previous activity by using the elimination method

the two equations from the previous activity are given below

k + a = 500 (1)
3K + 10A equals 3,600 (2)

which equation has at least one of its variables with a 1 as it's coefficient?
​

Answer 1

The value of a=300 and value of k=200

If you solve the above system of equations by elimination method, you will get the same values of a and k.

In Equation 1
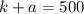`k+a=500` both variables k has 1 as their coefficient.

Explanation:

We need to solve the system of equations using substitution method

The equation are:

`k + a = 500--eq(1)\\3k + 10a = 3,600 --eq(2)`

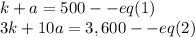
For substitution method, we find value of k from equation 1 and put in equation 2

`From \ eq(1) \ we \ get\\k=500-a`

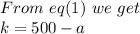
Putting it in eq(2)

`3k+10a=3600\\Put \ k=500-a\\3(500-a)+10a=3600\\1500-3a+10a=3600\\7a=3600-1500\\7a=2100\\a=(2100)/(7)\\a=300`

So, we get value of a = 300

Now finding value of k by putting value of a in equation
`k=500-a`

`k=500-a\\Putting \ a \ =500\\k=500-300\\k=200`

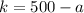
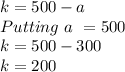
So, we get value of k =200

The value of a=300 and value of k=200

If you solve the above system of equations by elimination method, you will get the same values of a and k.

In Equation 1
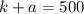`k+a=500` both variables k has 1 as their coefficient.