Question

X + x2 - 5x -5 = 0
state the possible rational zeros and find all the zeros of the polynomial

Answer 1

The zeros of the polynomial are -1 and 5

Explanation:

Quadratic Equation Solving

The standard representation of a quadratic equation is:

`ax^2+bx+c=0`

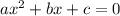
where a,b, and c are constants.

Solving with the quadratic formula:

`\displaystyle x=(-b\pm √(b^2-4ac))/(2a)`

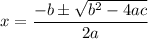
We have the following equation to solve:

`x+x^2-5x-5=0`

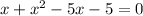
Before attempting to solve it, we must simplify the equation.

Collecting like terms and reordering:

`x^2-4x-5=0`

Here: a=1, b=-4, c=-5

The discriminant of this quadratic equation is:

`d=b^2-4ac`

`d=(-4)^2-4(1)(-5)=16+20=36`

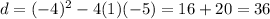
Given d is positive, the equation has two roots, and since d is a perfect square, both roots are rational.

Applying the formula:

`\displaystyle x=(4\pm √(36))/(2(1))`

`\displaystyle x=(4\pm 6)/(2)`

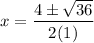
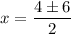
Dividing by 2:

`x=2\pm 3`

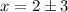
Separating both roots:

x = 2 + 3 = 5

x = 2 - 3 = -1

The zeros of the polynomial are -1 and 5