Question

Which is the equation of the parabola that

opens to the right, has a focus at (3.0), and
has a directrix at x=-3?

Answer 1

The equation of the parabola will be:

• 
  `\:y^2=12x`

Explanation:

The vertex (h, k) is halfway between the directrix and focus.

Find the x coordinate of the vertex using the formula

x = (x-coordinate of focus + directrix)/2

= (3-3)/2

= 0/2

=0

The y -coordinate will be the same as the y-coordinate of the focus.

so the vertex will be: (0, 0)

Finding the distance from the focus to the vertex

The distance from the focus to the vertex and from the vertex to the directrix is |p|.

Subtract the x coordinate of the vertex from the x -coordinate of the focus to find p .

`p=3-0`

`p=3`

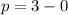
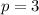
Substitute in the known values for the variables into the equation

`\left(y-k\right)^2=4p\left(x-h\right)`

`\left(y-0\right)^2=4\left(3\right)\left(x-0\right)`

`\:y^2=12x`

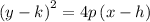
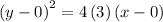
Therefore, the equation of the parabola will be:

• 
  `\:y^2=12x`