Question

A parabolic arch sculpture is on top of a city bank. A model of the arch is y = −0.005x2 + 0.3x where x and y are in feet.

The image is of a rectangle which represents the building of a Bank and its height is 30 feet. On top of it a semi circle is placed whose diameter is equal to the width of the rectangle.

a. What is the distance from the highest point of the arch to the ground?
b. What is the width of the bank?

A. a. 34.5 feet
b. 60 feet
B. a. 4.5 feet
b. 60 feet
C. a. 4.5 feet
b. 30 feet
D. a. 34.5 feet
b. 30 feet

Answer 1

A. a. 34.5 feet

b. 60 feet

Explanation:

Parabola equation

`y=-0.005x^2+0.3x`

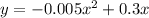
Differentiating with respect to x we get

`(dy)/(dx)=-0.01x+0.3`

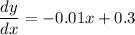
Equating with zero

`-0.01x+0.3=0\\\Rightarrow -0.01x=-0.3\\\Rightarrow x=(0.3)/(0.01)\\\Rightarrow x=30`

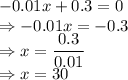
Double derivative of the parabolic equation

`(d^2y)/(dx^2)=-0.01<0`

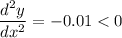
So,
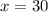`x=30` is maximum.

`y=-0.005* 30^2+0.3* 30\\\Rightarrow y=4.5`

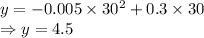
So, the maximum height of the arch will be 4.5 feet.

From the ground the highest point of the arch will be
`30+4.5=34.5\ \text{ft}`

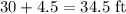
We are taking the x axis as the width of the bank.

`0=-0.005x^2+0.3x\\\Rightarrow 0.005x^2=0.3x\\\Rightarrow x=(0.3)/(0.005)\\\Rightarrow x=60`

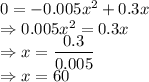
So, the width of the bank will be 60 feet.