Question

A company has a $150 budget to provide lunch for its 20 employees. The options are to provide either roast beef sandwiches, which cost $5 apiece, or tuna sandwiches, which also cost $5 apiece. The company also wants to use the entire budget. Suppose r represents the number of roast beef sandwiches it provides and t represents the number of tuna sandwiches. Which statement is correct?

The company can provide lunch for all 20 employees and use the entire budget because there is a solution to the system of equations r minus t = 20 and 5 r + 5 t = 150.
The company can provide lunch for all 20 employees and use the entire budget because there is a solution to the system of equations r + t = 20 and 5 r + 5 t = 150.
The company cannot provide lunch for all 20 employees and use the entire budget because there is no solution to the system of equations r minus t = 20 and 5 r + 5 t = 150.
The company cannot provide lunch for all 20 employees and use the entire budget because there is no solution to the system of equations r + t = 20 and 5 r + 5 t = 150.

Answer 1

D.) The company cannot provide lunch for all 20 employees and use the entire budget because there is no solution to the system of equations r+t=20 and 5r+5t=150

Explanation:

The given information says that the total amount of lunch bought should equal $150 when both options cost $5:

`5r+5t=150`

It also says that the food should feed all 20 employees:

`r+t=20`

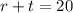
This is now a system. Solve by substitution.

Solve the second equation for r. Use inverse operations to isolate the variable by subtracting t from both sides:

`r+t-t=20-t\\\\r=20-t`

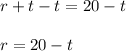
Now insert this value of r into the first equation:

`5(20-t)+5t=150`

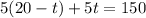
Simplify the equation. Use the distributive property:

`5(20)+5(-t)+5t=150\\\\100-5t+5t=150`

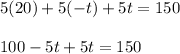
Cancel the terms:

`100\\eq 150`

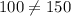
100 does not equal 150, so there is no solution to the system.

:Done