Question

Please answer this question, i request

If cot θ = 7/8 , evaluate :-
(1 + sin θ)(1 – sin θ)/(1 + cos θ)(1 - cos θ)​

Answer 1

`{\large{\textsf{\textbf{\underline{\underline{Given :}}}}}}`

`\star \: \tt \cot \theta = (7)/(8)`

`{\large{\textsf{\textbf{\underline{\underline{To \: Evaluate :}}}}}}`

`\star \: \tt ((1 + \sin \theta)(1 - \sin \theta) )/((1 + \cos \theta) (1 - \cos \theta) )`

`{\large{\textsf{\textbf{\underline{\underline{Solution :}}}}}}`

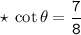
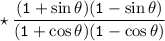
Consider a
`\triangle` ABC right angled at C and
`\sf \angle \: B = \theta`

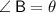
Then,

‣ Base [B] = BC

‣ Perpendicular [P] = AC

‣ Hypotenuse [H] = AB

`\therefore \tt \cot \theta = (Base)/( Perpendicular) = (BC)/(AC) = (7)/(8)`

Let,

Base = 7k and Perpendicular = 8k, where k is any positive integer

In
`\triangle` ABC, H² = B² + P² by Pythagoras theorem

`\longrightarrow \tt {AB}^(2) = {BC}^(2) + {AC}^(2)`

`\longrightarrow \tt {AB}^(2) = {(7k)}^(2) + {(8k)}^(2)`

`\longrightarrow \tt {AB}^(2) = 49{k}^(2) + 64{k}^(2)`

`\longrightarrow \tt {AB}^(2) = 113{k}^(2)`

`\longrightarrow \tt AB = \sqrt{113 {k}^(2) }`

`\longrightarrow \tt AB = \red{ √(113) \: k}`

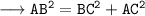
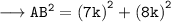
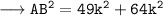
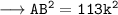
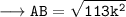
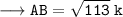
Calculating Sin
`\sf \theta`

`\longrightarrow \tt \sin \theta = (Perpendicular)/(Hypotenuse)`

`\longrightarrow \tt \sin \theta = (AC)/(AB)`

`\longrightarrow \tt \sin \theta = \frac{8 \cancel{k}}{ √(113) \: \cancel{ k } }`

`\longrightarrow \tt \sin \theta = \purple{ (8)/( √(113) ) }`

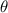
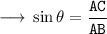
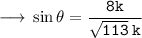
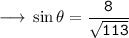
Calculating Cos
`\sf \theta`

`\longrightarrow \tt \cos \theta = (Base)/(Hypotenuse)`

`\longrightarrow \tt \cos \theta = (BC)/( AB)`

`\longrightarrow \tt \cos \theta = \frac{7 \cancel{k}}{ √(113) \: \cancel{k } }`

`\longrightarrow \tt \cos \theta = \purple{ (7)/( √(113) ) }`

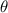
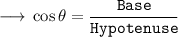
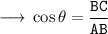
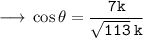
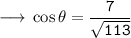
Solving the given expression :-

`\longrightarrow \: \tt ((1 + \sin \theta)(1 - \sin \theta) )/((1 + \cos \theta) (1 - \cos \theta) )`

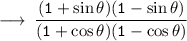
Putting,

• Sin
`\sf \theta` =
`(8)/( √(113) )`

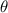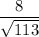
• Cos
`\sf \theta` =
`(7)/( √(113) )`

`\longrightarrow \: \tt ( \bigg(1 + (8)/( √(133)) \bigg) \bigg(1 - (8)/( √(133)) \bigg) )/(\bigg(1 + (7)/( √(133)) \bigg) \bigg(1 - (7)/( √(133)) \bigg))`

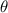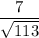
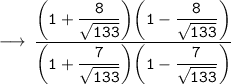
Using (a + b ) (a - b ) = a² - b²

`\longrightarrow \: \tt \frac{ { \bigg(1 \bigg)}^(2) - { \bigg( (8)/( √(133) ) \bigg)}^(2) }{ { \bigg(1 \bigg)}^(2) - { \bigg( (7)/( √(133) ) \bigg)}^(2) }`

`\longrightarrow \: \tt (1 - (64)/(113) )/( 1 - (49)/(113) )`

`\longrightarrow \: \tt ( (113 - 64)/(113) )/( (113 - 49)/(113) )`

`\longrightarrow \: \tt { \frac { (49)/(113) }{ (64)/(113) } }`

`\longrightarrow \: \tt { (49)/(113) }÷{ (64)/(113) }`

`\longrightarrow \: \tt \frac{49}{ \cancel{113}} * \frac{ \cancel{113}}{64}`

`\longrightarrow \: \tt (49)/(64)`

`\qquad \: \therefore \: \tt ((1 + \sin \theta)(1 - \sin \theta) )/((1 + \cos \theta) (1 - \cos \theta) ) = \pink{(49)/(64) }`

`\begin{gathered} {\underline{\rule{300pt}{4pt}}} \end{gathered}`

`{\large{\textsf{\textbf{\underline{\underline{We \: know :}}}}}}`

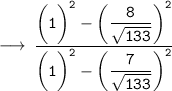
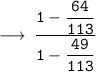
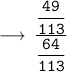
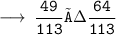
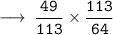
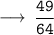
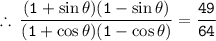
✧ Basic Formulas of Trigonometry is given by :-

`\begin{gathered}\begin{gathered}\boxed { \begin{array}{c c} \\ \bigstar \: \sf{ In \:a \:Right \:Angled \: Triangle :} \\ \\ \sf {\star Sin \theta = (Perpendicular)/(Hypotenuse)} \\\\ \sf{ \star \cos \theta = ( Base )/(Hypotenuse)}\\\\ \sf{\star \tan \theta = (Perpendicular)/(Base)}\\\\ \sf{\star \cosec \theta = (Hypotenuse)/(Perpendicular)} \\\\ \sf{\star \sec \theta = (Hypotenuse)/(Base)}\\\\ \sf{\star \cot \theta = (Base)/(Perpendicular)} \end{array}}\\\end{gathered} \end{gathered}`

`{\large{\textsf{\textbf{\underline{\underline{Note :}}}}}}`

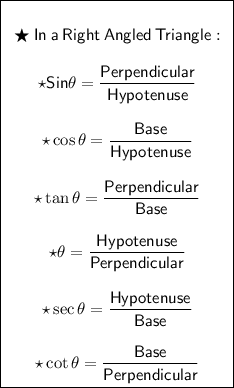
✧ Figure in attachment

`\begin{gathered} {\underline{\rule{200pt}{1pt}}} \end{gathered}`