Question

Which polynomial function could be represented by the graph below?

A.
`f(x) = x^2 - 4x`

B.
`f(x) = x^2 + 4x`

C.
`f(x) = -x^2 - 4x`

D.
`f(x) = -x^2 + 4x`

Answer 1

`f(x) = {x}^(2) + 4x`

Explanation:

The graph is concave up, this means that the leading term x^2 is positive.

`f(x) = {x}^(2) + 4x`

`y = {x}^(2) + 4x`

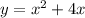
For the x intercept, let y = 0

`{x}^(2) + 4x = 0`

`x(x + 4) = 0`

`x = 0 \: \: \: or \: \: \: \: x = - 4`

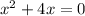
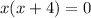
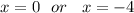
The x intercepts are:

(0 , 0) and (-4 , 0)

For the y intercept, let x = 0

`y = {0}^(2) + 4(0) = 0`

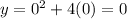
y intercept :

(0, 0)

For the turning point:

`t.p = (x1 + x2)/(2)`

`t.p = (0 + ( - 4))/(2) = - 2`

`f( - 2) = {( - 2)}^(2) + 4( - 2) = - 4`

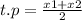
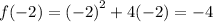
Turning point:

(-2 , -4)

If you connect all these coordinates you will get the parabola shown in the picture.