Question

S 2. Let f(x) = x - k√x

a. Find a value of k such that the function has a critical point at x = 25.
b. Is the above critical point a local maximum, local minimum or neither? Show calculus to support your answer.​

Answer 1

a. A critical point at x = 25 would mean f'(25) = 0 or doesn't exist. We have derivative

`f(x) = x - k \sqrt x \implies f'(x) = 1 - \frac k{2\sqrt x}`

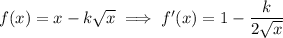
so that

`f'(25) = 1 - \frac k{2√(25)} = 1 - \frac k{10} = 0 \implies \boxed{k=10}`

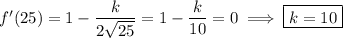
b. Taking the second derivative, we get

`f''(x) = \frac k{4 x^(3/2)} = \frac5{2 x^(3/2)}`

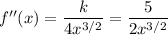
At x = 25, the second derivative has a positive sign,

`f''(25) = \frac 5{2 * 25^(3/2)} = \frac 5{2*5^3} = \frac1{50} > 0`

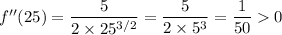
which means f(x) is concave upward around x = 25, so this critical point is a local minimum.