Question

Charlotte works in a calling center making appointments for a local lawn care service. She earns $40 each full workday plus an additional $2 for each appointment that she schedules. Today, Charlotte needs to earn at least $75. Write an inequality to describe this situation. In two or more complete sentences, describe the solution set of this inequality and what it means for Charlotte.

Answer 1

Since she makes $2 for every appointment she makes we would need to use 40+2n so she would get $2 per appointment no matter how many appointments she makes. Also, we wouldn't use an equal sign because they didn't say she needed to earn exactly $75. They said she needed to earn "at least" $75. At least means equal to or greater than ≥. So the inequality would be 2n+40≥75. PRO TIP: Any time it asks you to write an inequality you will use either <, >, ≤, or ≥ not an =.An equation uses =, an inequality uses the other symbols

Answer 2

x = number of appointments

y = total amount earned in dollars

The total earnings equation is y = 2x+40

The 2x is from her earning $2 per appointment. If she makes x of them, then she earns 2x dollars. This is on top of the $40 from working the full day.

She wants to earn at least $75. This means she wants to earn $75 or more.

This means,

`y \ge 75\\\\2x+40 \ge 75\\\\2x \ge 75-40\\\\2x \ge 35\\\\x \ge (35)/(2)\\\\x \ge 17.5`

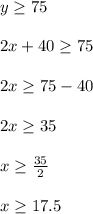
Since x is the number of appointments, and we can't have a fractional number of appointments, we must round up to x = 18. This is the lowest number of appointments she can do and earn $75 or larger.

If x = 17, then

y = 2x+40 = 2*17+40 = 34+40 = 74

which is not 75 or larger

But if x = 18, then

y = 2x+40 = 2*18+40 = 36+40 = 76

which is larger than 75, so we've cleared the hurdle.

We can say the solution set is
`x \ge 18` where x is a whole number. So she could book x = 18, x = 19, x = 20, x = 21, etc as the number of appointments to reach her goal.

In summary, she must schedule at least 18 appointments to earn $75 or more.