Question

I needs help with it please ​

Answer 1

(i) (0, -32)

(ii) (-4, 0) and (8, 0)

(iii) x = 2

(iv) (2, -36)

(v) (2, -36) minimum

Explanation:

Given quadratic equation:

`y=x^2-4x-32`

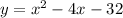
Part (i)

The y-intercept is the point at which the curve crosses the y-axis.

To find the y-intercept, substitute x = 0 into the given equation:

`\implies (0)^2-4(0)-32=-32`

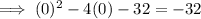
Therefore, the y-intercept is at (0, -32)

Part (ii)

The zeros are the points at which the curve crosses the x-axis.

To find the zeros, substitute y = 0 into the given equation and factor:

`\implies x^2-4x-32=0`

`\implies x^2-8x+4x-32=0`

`\implies x(x-8)+4(x-8)=0`

`\implies (x+4)(x-8)=0`

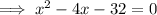
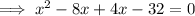
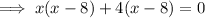
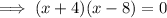
Therefore:

`(x+4)=0 \implies x=-4`

`(x-8)=0 \implies x=8`

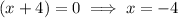
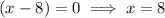
So the zeros are (-4, 0) and (8, 0)

Part (iii)

The axis of symmetry is a vertical straight line that divides the curve into two symmetrical parts. The axis of symmetry is the x-value of the mid-point of the zeros.

`\sf \implies midpoint=(8+(-4))/(2)=2`

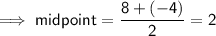
Therefore, the axis of symmetry is: x = 2

Part (iv)

The vertex is the turning point of the parabola.

If the leading coefficient is positive, the parabola opens upwards and the vertex is the minimum point.

If the leading coefficient is negative, the parabola opens downwards and the vertex is the maximum point.

The axis of symmetry is the x-value of the vertex.

To find the y-value, substitute x = 2 into the equation:

`\implies (2)^2-4(2)-32=-36`

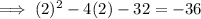
Therefore, the vertex is (2, -36)

Part (v)

The optimal value is also known as the vertex.

Therefore, the optimal value is (2, -36).

As the leading coefficient of the given quadratic equation is positive, the parabola opens upwards and so the optimal value is a minimum.