Question

A satellite orbits earth with a mean altitude of 361 km. If the orbit is circular, what are the satellite's time period and speed?

Answer 1

v = 7.69 x 10³ m/s = 7690 m/s

T = 5500 s = 91.67 min = 1.53 h

Step-by-step explanation:

In order for the satellite to orbit the earth, the force of gravitation on satellite must be equal to the centripetal force acting on it:

`F_(gravitation)= F_(centripetal)\\\\(GM_(s) M_(E))/(r^2) = (M_(s) v^2)/(r)\\\\(GM_(E))/(r) = v^2\\\\v = \sqrt{(GM_(E))/(r) } \\\\`

where,

G = Universal Gravitational Constant = 6.67 x 10⁻¹¹ N.m²/kg²

Me = Mass of Earth = 5.97 x 10²⁴ kg

r = distance between the center of Earth and Satellite = Radius of Earth + Altitude = 6.371 x 10⁶ m + 0.361 x 10⁶ m = 6.732 x 10⁶ m

v = orbital speed = ?

Therefore,

`v = \sqrt{((6.67 x 10^(-11)N.m^2/kg^2)(5.97 x 10^(24) kg))/(6.732 x 10^6 m) }\\\\`

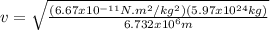
v = 7.69 x 10³ m/s

For time period satellite completes one revolution around the earth. It means that the distance covered by satellite is equal to circumference of circle at the given altitude.

So, its orbital speed can be given as:

`v = (Circumference of Circle at Given Altitude)/(T)\\\\v = (2\pi r)/(T)\\\\`

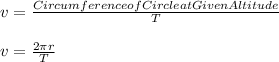
where,

T = Time Period of Satellite = ?

Therefore,

`T = (2\pi r)/(v)\\\\T = ((2\pi )(6.732 x 10^6 m)/(7.69 x 10^3 m/s)\\\\`

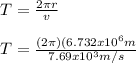
T = 5500 s = 91.67 min = 1.53 h