We know that side NM is parallel to side XZ. If we consider side NY the transversal for these parallel lines, we create angle pairs. Using the corresponding angles theorem, we can state that
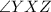 is congruent to
is congruent to
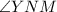 . We know that angle XYZ is congruent to angle XYZ by the reflexive property. Therefore, triangle XYZ is similar to triangle to triangle NYM by the angle-angle similarity theorem.
. We know that angle XYZ is congruent to angle XYZ by the reflexive property. Therefore, triangle XYZ is similar to triangle to triangle NYM by the angle-angle similarity theorem.