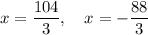Answer:
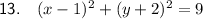
center = (1, -2)
radius = 3
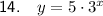
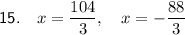
Explanation:
Question 13
Equation of a circle

(where (a, b) is the center and r is the radius)
Given equation:
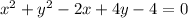
To rewrite the given equation in graphing form, first add 4 to both sides of the equation and rearrange the variables:
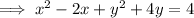
Add the square of half the coefficients of the x and y terms to both sides:

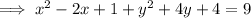
Finally, factor both trinomials:
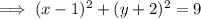
Now compare the equation in graphing form to the general equation of a circle to find the center and radius:
⇒ a = 1 and b = -2 ⇒ center = (1, -2)
⇒ r² = 9 ⇒ radius = √9 = 3
Question 14
General form of an exponential function:

(where a and b are constants to be found)
Given points on the curve:
Substitute the given points into the general form of the equation to create two equations:
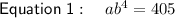

Divide Equation 2 by Equation 1 to eliminate a, then solve for b:
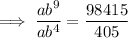
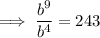
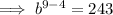
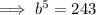
![\implies b=\sqrt[5]{243}](https://img.qammunity.org/2023/formulas/mathematics/college/ihj0mk21r0625avbrpcw1oszu5gx5wshtk.png)

Substitute the found value of b into one of the equations and solve for a:
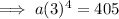
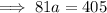
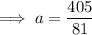

Therefore, the exponential equation that passes through (4, 405) and (9, 98415) is:
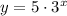
Question 15
Given equation:

Isolate the absolute value by subtracting 2 from both sides:
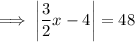
Set the contents of the absolute value to positive and negative and solve for x:
Positive absolute value:
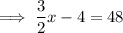
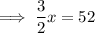
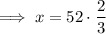
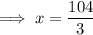
Negative absolute value:
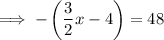

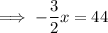
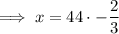
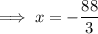
Therefore, the solution to the equation is: