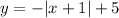Question

NO LINKS!!! What is the equation of these two graphs?​

Answer 1

`\textsf{1.} \quad y=-(1)/(30)x^2+(1)/(2)x+(68)/(15)\:\:\textsf{ where}\:\:x \geq (15-√(769))/(2)\\\\\quad \textsf{or} \quad y=2√(x+5)`

`\textsf{2.} \quad y=-|x+1|+5`

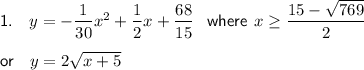
Explanation:

Question 1

Method 1 - modelling as a quadratic with restricted domain

Assuming that the points given on the graph are points that the curve passes through, the curve can be modeled as a quadratic with a limited domain. Please note that as the x-intercept has not been defined on the graph, I am not including this in this first method.

Standard form of a quadratic equation:

`y=ax^2+bx+c`

Given points:

• (-4, 2)
• (-1, 4)
• (4, 6)

Substitute the given points into the equation to create 3 equations:

Equation 1 (-4, 2)

`\implies a(-4)^2+b(-4)+c=2`

`\implies 16a-4b+c=2`

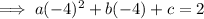
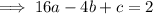
Equation 2 (-1, 4)

`\implies a(-1)^2+b(-1)+c=4`

`\implies a-b+c=4`

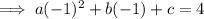
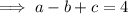
Equation 3 (4, 6)

`\implies a(4)^2+b(4)+c=6`

`\implies 16a+4b+c=6`

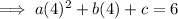
Subtract Equation 1 from Equation 3 to eliminate variables a and c:

`\implies (16a+4b+c)-(16a-4b+c)=6-2`

`\implies 8b=4`

`\implies b=(4)/(8)`

`\implies b=(1)/(2)`

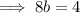
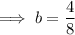
Subtract Equation 2 from Equation 3 to eliminate variable c:

`\implies (16a+4b+c)-(a-b+c)=6-4`

`\implies 15a+5b=2`

`\implies 15a=2-5b`

`\implies a=(2-5b)/(15)`

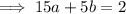
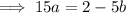
Substitute found value of b into the expression for a and solve for a:

`\implies a=(2-5((1)/(2)))/(15)`

`\implies a=-(1)/(30)`

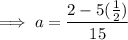
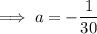
Substitute found values of a and b into Equation 2 and solve for c:

`\implies a-b+c=4`

`\implies -(1)/(30)-(1)/(2)+c=4`

`\implies c=(68)/(15)`

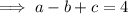
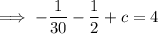
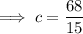
Therefore, the equation of the graph is:

`y=-(1)/(30)x^2+(1)/(2)x+(68)/(15)`

`\textsf{with the restricted domain}: \quad x \geq (15-√(769))/(2)`

Method 2 - modelling as a square root function

Assuming that the points given on the graph are points that the curve passes through, and the x-intercept should be included, we can model this curve as a square root function.

Given points:

• (-4, 2)
• (-1, 4)
• (4, 6)
• (0, -5)

The parent function is:

`y=√(x)`

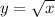
Translated 5 units left so that the x-intercept is (0, -5):

`\implies y=√(x+5)`

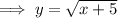
The curve is stretched vertically, so:

`\implies y=a√(x+5) \quad \textsf{(where a is some constant)}`

To find a, substitute the coordinates of the given points:

`\implies a√(-4+5)=2`

`\implies a=2`

`\implies a√(-1+5)=4`

`\implies 2a=4`

`\implies a=2`

`\implies a√(4+5)=6`

`\implies 3a=6`

`\implies a=2`

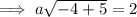
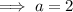
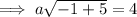
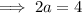
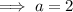
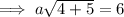
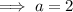
As the value of a is the same for all points, the equation of the line is:

`y=2√(x+5)`

Question 2

Vertex form of an absolute value function

`f(x)=a|x-h|+k`

where:

• (h, k) is the vertex
• a is some constant

From inspection of the given graph:

• vertex = (-1, 5)
• point on graph = (0, 4)

Substitute the given values into the function and solve for a:

`\implies a|0-(-1)|+5=4`

`\implies a+5=4`

`\implies a=-1`

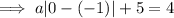
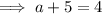
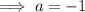
Substituting the given vertex and the found value of a into the function, the equation of the graph is:

`y=-|x+1|+5`