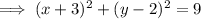Answer:
Explanation:
Equation of a circle
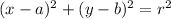
where:
- (a, b) is the center
- r is the radius
From inspection of the diagram, the center of the circle appears to be at point (-3, 2), although this is not very clear. Therefore, a = -3 and b = 2.
Substitute these values into the general form of the equation of a circle:
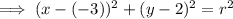
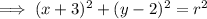
Again, from inspection of the diagram, the maximum vertical point of the circle appears to be at y = 5. Therefore, to calculate the radius, subtract the y-value of the center point from the y-value of the maximum vertical point:
⇒ radius (r) = 5 - 2 = 3
Substitute the found value of r into the equation:
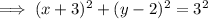
Therefore, the final equation of the given circle is: