Question

A jet liner must reach a speed of 82 m/s for takeoff. If the

runway is 1500 m long, what acceleration must the jet
have?

Answer 1

The acceleration that the jet liner that must have is 2.241 meters per square second.

Step-by-step explanation:

Let suppose that the jet liner accelerates uniformly. From statement we know the initial (
`v_(o)`) and final speeds (
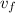`v_(f)`), measured in meters per second, of the aircraft and likewise the runway length (
`d`), measured in meters. The following kinematic equation is used to calculate the minimum acceleration needed (
`a`), measured in meters per square second:

`a = (v_(f)^(2)-v_(o)^(2))/(2\cdot d)`

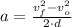
If we know that
`v_(o) = 0\,(m)/(s)`,
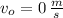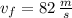`v_(f) = 82\,(m)/(s)` and
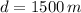`d = 1500\,m`, then the acceleration that the jet must have is:

`a = (\left(82\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2))/(2\cdot (1500\,m))`

`a = 2.241\,(m)/(s^(2))`

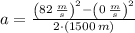
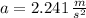
The acceleration that the jet liner that must have is 2.241 meters per square second.