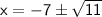Answer:
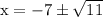
Explanation:
Solve for x over the real numbers:
 x² + 14x + 38 = 0
x² + 14x + 38 = 0
Subtract 38 from both sides:
 x² + 14x + 38 - 38 = 0 - 38
x² + 14x + 38 - 38 = 0 - 38
 x² + 14x = -38
x² + 14x = -38
Add 49 to both sides:
 x² + 14x + 49 = 49 - 38
x² + 14x + 49 = 49 - 38
 x² + 14x + 49 = 11
x² + 14x + 49 = 11
Write the left hand side as a square:
 x² + 7x + 7x + 49 = 11
x² + 7x + 7x + 49 = 11
 x(x + 7) + 7(x + 7) = 11
x(x + 7) + 7(x + 7) = 11
 (x + 7)(x + 7) = 11
(x + 7)(x + 7) = 11
 (x + 7)² = 11
(x + 7)² = 11
Take the square root of both sides:

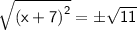

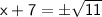
Subtract 7 from both sides: