Answer:
The original length of the new candle is 10 inches
Explanation:
The form of the linear function is y = m x + b, where
- m is the slope of the line
- b is the y-intercept value y at x = 0
∵ L represents the length of the candle remeaning unburned in inches
∵ t represents the time after the candle was lit in hours
∵ The relationship between L and t is linear
→ Put it in the form of the equation above
∴ L = m t + b, where b is the original length of the new candle
→ Use the table to find m
∵ m =
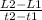
∵ (1, 9) and (6, 4) are two points in the given table
∴ t1 = 1 and L1 = 9
∴ t2 = 6 and L2 = 4
→ Substitute them in the rule of m above
∵ m =
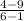 =
=
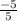 = -1
= -1
∴ m = -1
→ Substitute it in the equation above
∵ L = -1(t) + b
∴ L = -t + b
→ To find b substitute t by 1 and L by 9
∵ 9 = -(1) + b
∴ 9 = -1 + b
→ Add 1 to both sides
∵ 9 + 1 = -1 + 1 + b
∴ 10 = b
∵ b is the original length of the new candle
∴ The original length of the new candle is 10 inches