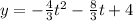Question

The distance of a golf ball from the hole can be represented by the right side of a parabola with vertex (−1, 8). The ball reaches the hole 1 second after it is hit, at time 0. What is the equation of the parabola, in vertex form, that represents the ball's distance from the hole, y, at time x

Answer 1

The required equation is:

`y = -(4)/(3)t^2 -(8)/(3)t + 4`

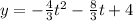
Step-by-step explanation:

Let us assume that the hole is at y = 0m, with x as the time.

From the question we have (-1s, 8m) as the vertex (here x being the time variable is supposed to be in seconds and y being the distance variable is supposed to be in meters)

At x = 1s, the ball gets to the hole, therefore we have point (1s, 0m)

We know that the vertex of the parabola y = ax² + bx + c is at

`x =(-b)/(2a)`

therefore we have:

`-1 = (-b)/(2a)`

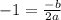
We then have the following equations:

`8 = a* -1^2 + b* -1 + c`

`0 = a* -1^2 + b* 1 + c`

`-1 = (-b)/(2a)`

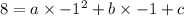
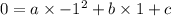
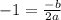
From the 3rd equation we have

1 X 2a = b.

Therefore we have:

`8 = a* -1^2 - 1* 2a*1 + c`

`0 = a* 1^2 + 1 *2a* 1 + c`

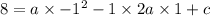
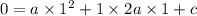
We can simplify both equations and get:

`8 = a*( -1^2 - 2s^2) + c = -a* 3^2 + c`

`0 = a*(1^2 + 2^2) + c = a* 3^2 + c`

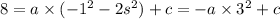
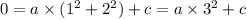
The first equation now becomes:

`8 = -a* 3 - a* 3 = -a* 6`

`a = frac{8}{-6} = -(4)/(3)`

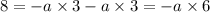
With a, we can find the values of c and b.

`c = -a*3 = -(-(4)/(3))*3 = 4`

`b = 1* 2a = 1* 2(-(4)/(3))= -(8)/(3)`

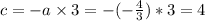
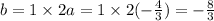
Then the equation is:

`y = -(4)/(3)t^2 -(8)/(3)t + 4`