Question

Consider the following IP problem:

Maximum Z= 5x1+x2

subject to
-x1+2x2 <=4
x1-x2 <=4
4x1+ x2 <=12

and
x1 >=0, x2>=0
x1, x2 are integers

a. Solve this problem graphically.
b. Solve the LP relaxation graphically. Round this solution to the nearest integer solution and check whether it is feasible. Then enumerate all the rounded solutions by rounding the solution for the LP relaxation in all possible ways (i.e., by rounding each noninteger value both up and down). For each rounded solution, check for feasibility and, if feasible, calculate Z. Are any of these feasible rounded solutions optimal for the IP problem?

Answer 1

`(3,0)`

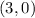
Explanation:

The integer points which fall in the common region bounded by the lines are

`(0,2),(2,3),(3,0)`

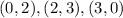
Since, one of the points is
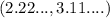`(2.22...,3.11....)` we round it to
`(2,3)`

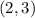
If we round up then the point will be
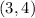`(3,4)` which does not fall in the bounded region.

Also
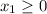`x_1\geq 0` and
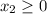`x_2\geq 0` no negative values are considered.

Applying in the values in the LP problem
`Z=5x_1+x_2`

`Z=5* 0+2\\\Rightarrow Z=2`

`Z=5* 2+3\\\Rightarrow Z=13`

`Z=5* 3+0\\\Rightarrow Z=15`

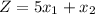
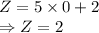
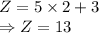
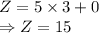
So, the LP problem is maximum at point
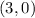`(3,0)`.