Question

A toy rocket is launched straight up by using a spring. The rocket is initially pressed down on the spring so that the spring is compressed by 9 cm. If the spring constant is 830 N/m and the mass of the rocket is 50 g, how high will the rocket fly?

Answer 1

6.86 meters

Step-by-step explanation:

Let the compression of the string be represented by x, and the height of projection of the toy rocket be represented by h.

So that;

x = 9 cm = 0.09 m

In its rest position (i.e before the launch), the spring has a stored potential energy which is given as;

PE =
`(1)/(2)` K
`x^(2)`

=
`(1)/(2)` x 830 x
`(0.09)^(2)`

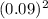
= 415 x 0.0081

= 3.3615

The potential energy in the string = 3.36 Joules

Also,

PE = mgh

where: m is the mass, g is the gravitational force and h the height.

m = 50 g = 0.05 kg, g = 9.8 m
`s^(-2)`

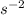
Thus,

PE = 0.05 x 9.8 x h

3.3615 = 0.05 x 9.8 x h

3.3615 = 0.49h

⇒ h =
`(3.3615)/(0.49)`

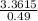
= 6.8602

The height of the toy rocket would be 6.86 meters.