Question

It rains on Paradise Island on 40% of the days. The chance of rain is independent from day to day. A travel agent is signing people up to go on a 5-day tour of the island. She wants to know the chance of getting at least two consecutive days of rain at any time during the 5 days. To determine this, a simulation will be used.

Answer 1

The probability that it will rain in atleast two consecutive days will be 0.167936.

Explanation:

Since it rains on 40% of the days, then the probability of it raining on each day is

This follows a binomial distribution

Since it's a five-day tour and they want to know the probability that rain falls in atleast TWO CONSECUTIVE days then we have to consider 2 days as one, as we do in combination problems, so that they are always together before we use in our binomial probability density function.

Our Probability Density Function is given as

`P(X) = \binom{n}{x} p^x * q^(n-x)`

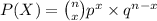
Where p is probability of raining and q = 1 - p is probability of not raining.

Our n is 4 since we are considering two days as one.

We are looking the P(X≥2) = 1 – P(X<2) = 1 – [P(X = 0) + P(X = 1).

`P(X = 0) = \binom{4}{0} 0.4^0 * 0.6^4 = 0.1296`

`P(X = 1) = \binom{4}{1} 0.4^1 * 0.6^3 = 4* 0.4 * 0.216 = 0.3456`

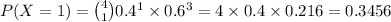
Therefore P(X≥2) = 1 – (0.1296 + 0.3456) = 0.5248.

Remember we combined two consecutive days that it will rain as one, their probabilities will be:

2! x 0.4 x 0.4 = 0.32

Therefore, the probability that it will rain in atleast two consecutive days will be

0.32 x 0.5248 = 0.167936