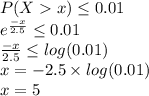Answer:
a) 0.2018
b)0.329
c)x=5
Explanation:
We are given that This process can be described using an exponential probability density function with a mean of 2.5.
So,
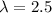

Where x>0 ,
 > 0
> 0
a) Find the probability that a customer has to wait more than 4 minutes.
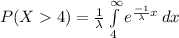

b)Find the probability that a customer is served within the first minute.
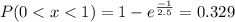
c)The manager wants to advertise that anybody who isn't served within a certain number of minutes gets a free hamburger. But she doesn't want to give away free hamburgers to more than 1% of her customers. What number of minutes should the advertisement use?