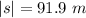Question

A 1800 kg car moves along a horizontal road at speed v₀ = 18.4 m/s. The road is wet, so the static friction coefficient between the tires and the road is only µ static = 0.188 and the kinetic friction coefficient is even lower, µ kinetic = 0.1316. The acceleration of gravity is 9.8 m/s². What is the shortest possible stopping distance for the car under such conditions? (neglect the reaction time of the driver and round your answer to 4 decimal places)

Answer 1

The shortest possible distance is
`|s| = 91.9 \ m`

Step-by-step explanation:

From the question we are told that

The mass of the car is
`m = 1800 \ kg`

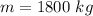
The speed along the horizontal road is
`v_o =u = 18.4 \ m/s`

The static friction coefficient is
`\mu_s = 0.188`

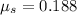
The kinetic friction coefficient is
`\mu_k = 0.1316`

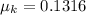
Generally the static frictional force acting on the car is mathematically represented as

`F_f = m * g * \mu_s`

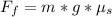
Generally the force propelling the car is mathematically represented as

`F = m * a`

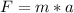
Here a is the maximum acceleration

at the point which the car stops ,

`F = F_f`

=>
`m * g * \mu_s = ma`

=>
`g * \mu_s =a`

=>
`a = 9.8 * 0.188`

=>
`a = 1.8424 \ m/s^2`

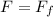
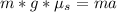
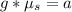
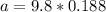
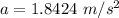
Generally from kinematic equation

`v^2 = u^2 + 2as`

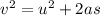
Here v is the final velocity of the car and the value is zero given that the car comes to rest

So

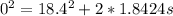
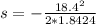
`0^2 = 18.4^2 + 2* 1.8424 s`

=>
`s = - (18.4^2)/(2 * 1.8424)`

=>
`|s| = 91.9 \ m`