Answer:
A) Ana y María e encuentran a las 8 hs 19 minutos 10 segundos (250 segundos después).
María y Ana se encuentran cuando aún faltan 1500 metros para llega al instituto.
B) Ana tendría que pedalear como mínimo para que María no la alcanzase antes de llegar al instituto a una velocidad de 6.857
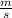 .
.
Step-by-step explanation:
A) Un movimiento es rectilíneo cuando un objeto describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo. En otras palabras, el Movimiento Rectilíneo Uniforme es una trayectoria recta, su velocidad es constante y su aceleración es nula.
Para una posición inicial x0 y una velocidad v que tiene el cuerpo a lo largo del movimiento, la posición para cualquier tiempo está dada por:
x(t)= x0 + v*t
Estableciendo el origen de referencia en el instituto, se tienen los siguientes valores:
- x0ana= 3 km= 3000 m
- x0maria= 3500 m
Por otro lado, Ana pedalea a 6 m/s y María a 8 m/s.
Entonces, como Ana y María se acercan al origen de referencia, la escuela, se la ecuación del movimiento para cada una de ellas es:
- xana= 3000 - 6*t
- xmaria= 3500 - 8*t
Ambas se encuentra cuando la posición de ellas sea la misma, esto es xana=xmaria. Entonces:
3000 -6*t= 3500 - 8*t
Resolviendo:
-6*t + 8*t= 3500 - 3000
2*t= 500
t= 500÷2
t=250 s= 4 minutos 10 segundos
Ana y María se encuentran a las 8 hs 19 minutos 10 segundos (250 segundos después).
Para conocer la posición en la que se encuentran debes sustituir el tiempo en la ecuación del movimiento de alguna de ellas:
xana=3000 - 6*250
xana= 1500 m
Es decir, María y Ana se encuentran cuando aún faltan 1500 metros para llega al instituto.
B) Para que esto ocurra Ana y María deben llegar al instituto al mismo tiempo. Entonces, el tiempo que tarda María en llegar a al origen de referencia, la escuela, es:
0= 3500 - 8*t
Resolviendo:
3500=8*t
3500÷8= t
437.5 segundos= t
Así que, si Ana 437.5 segundos o menos, María no la alcanzaría. Siendo la velocidad la relación entre el espacio recorrido por un objeto y el tiempo empleado para ello, entonces la velocidad de Ana se calcula como:
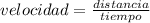
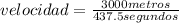
velocidad= 6.857
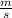
Ana tendría que pedalear como mínimo para que María no la alcanzase antes de llegar al instituto a una velocidad de 6.857
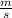 .
.