Question

A taxi driver had 27 fares to and from the airport last Monday. The price for a ride to the airport is $14, and the price for a ride from the airport is $7. The driver collected a total of $294 for the day. Let x represent the number of trips to the airport and y represent the number of trips from the airport. Write the ordered pair (x,y) that represents the solution in this situation.

Answer 1

(15, 12)

Explanation:

Let's generate two systems of equations that fit this scenario.

Number of trips to the airport = x

Number of trips from the airport = y

Total number of trips to and from the airport = 27

Thus:

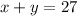`x + y = 27` => equation 1.

Total price for trips to the Airport = 14*x = 14x

Total price of trips from the airport = 7*y = 7y

Total collected for the day = $294

Thus:

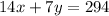`14x + 7y = 294` => equation 2.

Multiply equation 1 by 7, and multiply equation 2 by 1 to make both equations equivalent.

7 ×
`x + y = 27`

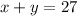
1 ×
`14x + 7y = 294`

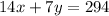
Thus:

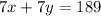`7x + 7y = 189` => equation 3

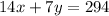`14x + 7y = 294` => equation 4

Subtract equation 4 from equation 3

-7x = -105

Divide both sides by -7

x = 15

Substitute x = 15 in equation 1

`x + y = 27`

`15 + y = 27`

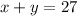
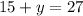
Subtract both sides by 15

`y = 27 - 15`

`y = 12`

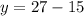
The ordered pair would be (15, 12)