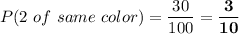Question

) 10 counters in a bag. 4 red, 3 green, 2 pink and 1 blue. Ella picks a counter at random from the bag, notes the colour and then puts it back in the bag. a) Ella uses this method to work out the probability of selecting 2 greens in a row. She writes: "There are four colours, so the probability of selecting a green is 1 4 + 1 4 = 2 4 , so the probability is 1 2 ." a) Make two criticisms of Ella's method. b) Calculate the probability of selecting two counters of the same colour. (

Answer 1

a) i) The probability depends on the total number of counters not on the number of colors.

ii) There are 10 number of counters not 4

b)
`(3)/(10)`

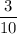
Explanation:

Given that:

Total number of counters in a bag = 10

Number of red counters = 4

Number of green counters = 3

Number of pink counters = 2

Number of blue counters = 1

a) Ella writes: "There are four colors, so the probability of selecting a green is
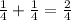`\frac{1}4 + \frac{1}4 = \frac{2}4` , so the probability is
`\frac{1}2`"

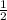Ella has considered the total type of counters here, which is 4.

But Ella must have considered total number of counters which is 10.

i) The probability depends on the total number of counters not on the number of colors.

ii) There are 10 number of counters not 4

b) There are 4 colors in the bag.

Formula for probability of an event E can be observed as:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

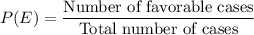
To select 2 counters of the same color:

`P(2\ red) = (4)/(10)* (4)/(10) = (16)/(100)`

`P(2\ green) = (3)/(10)* (3)/(10) = (9)/(100)`

`P(2\ pink) = (2)/(10)* (2)/(10) = (4)/(100)`

`P(2\ blue) = (1)/(10)* (1)/(10) = (1)/(100)`

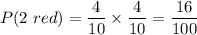
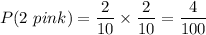
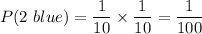
The required probability will be the sum of all 4 above probabilities:

`P(2\ of\ same\ color) = (30)/(100) = \bold{(3)/(10) }`