Question

EXPENSES: Camille has no more than $50.00 to spend each week for lunch and bus fare. Lunch costs $3.00 each day, and bus fare is $1.75 each ride. Write an inequality for this situation. Can Camille buy lunch 7 times and ride the bus 14 times in one​ week????

Answer 1

Inequality:
`3.00 L + 1.75B \leq 50`

She can afford to buy the lunch and bus rides

Explanation:

Given

`Maximum\ Amount = \$50.00`

`Lunch = \$3.00` daily

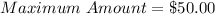
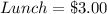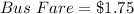`Bus\ Fare = \$1.75` daily

Solving (a) The inequality

Let bus ride be represented with B and Lunch be represented with L

If 1 bus ride costs $1.75, then

B bus ride would cost $1.75 * B

If 1 lunch costs $3.00, then

L lunch would cost $3.00 * L

Total Spending is then the sum of the above expression i.e.

$3.00 * L + $1.75 * B

The question says Camille can not spend more than $50.00.

This is represented by less than or equal to.

So, the expression is:

`3.00 * L + 1.75 * B \leq 50`

`3.00 L + 1.75B \leq 50`

Solving (b): Can she afford 7 lunch and 14 bus ride?

To do this, we simply substitute 7 for L and 14 for B

`3.00 * 7 + 1.75 * 14 \leq 50`

`21 + 24.5 \leq 50`

`45.5 \leq 50`

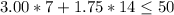
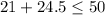
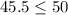
The above inequality is true.

Hence, she can afford to buy the lunch and bus rides