Question

2. A Se lanza un electrón con rapidez inicial v0 = 1.60×106 m/s hacia el interior de un campo uniforme entre las placas paralelas de la figura E21.33. Suponga que el campo entre las placas es uniforme y está dirigido verticalmente hacia abajo, y que el campo fuera de las placas es igual a cero. El electrón ingresa al campo en un punto equidistante de las dos placas. A) Si el electrón apenas elude la placa superior al salir del campo, encuentre la magnitud del campo eléctrico. B) Suponga que en la figura E21.33 el electrón es sustituido por un protón con la misma rapidez inicial v0. ¿Golpearía el protón una de las placas? Si el protón no golpea ninguna de las placas, ¿cuáles serían la magnitud y la dirección de su desplazamiento vertical, cuando sale de la región entre las placas? C) Compare las trayectorias que recorren el electrón y el protón, y explique las diferencias. D) Analice si es razonable ignorar los efectos de la gravedad para cada partícula.

Answer 1

A) E = 145.6 N / C , B) y= 2,8 10-7 m with a downward direction

C) he shape of the trajectory of the two particles is to simulate a parabola,

D) F_{e} /F_{g} = 10³⁴

Step-by-step explanation:

A) For this exercise we use Newton's second law to find the acceleration of the electron, where the force is electric

F = m a

- e E = m a

a = - e E / m

with the field directed downward, the acceleration is in the vertical upward direction.

We look for how much the electron moves with kinematics, in the x direction there is no acceleration,

x axis (parallel to plates)

x = v₀ t

t = x / v₀

y axis (perpendicular to plates)

y = y₀ +
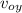`v_(oy)` t + ½ a t²

Let's take the zero of the system in the middle of the plates y₀ = 0, also the initial vertical velocity is zero (v_{oy} = 0) the width of the plate is known

y = ½ a t²

we substitute

y = ½ (e E /m) (x / v₀)²

y = ½ e x2 /m v₀² E

we look for the electric field

E = 2 m y v₀² / e x²

where to use this expression the length and width of the condenser must be known, suppose that the length is x = l = 1 cm = 1 10⁻² m and the width is y = 0.5 mm = 0.5 10⁻³ m

let's calculate

E = 2 9.1 10⁻³¹ 0.5 10⁻³ (1.6 10⁶)² / (1.6 10⁻¹⁹ (1 10⁻²)²)

E = 145.6 N / C

B) The electron is exchanged for a proton

Let's look for the vertical displacement, in this case as the proton has a positive charge it moves towards the bottom of the plates

y = ½ e x² / m v₀² E

y = ½ 1.6 10⁻¹⁹ 1 10⁻⁴ / (1.67 10⁻²⁷ (1.6 10⁶)² 145.6

y = 28.4375 10⁻⁸ m

since the distance between the plates is 0.5 10-3 m, the proton passes the condensate because its deflection is very small

In summary, its displacement is y= 2,8 10-7 m and with a downward direction (the same direction of the electric field)

C) The shape of the trajectory of the two particles is to simulate a parabola, but one for having a negative charge (electron) the force is upwards and the other for having a positive charge (proton) the trajectory is downwards

D) The force of gravity

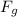`F_(g)` = G m M / R²

electron

Between the electron and the positive charges of the conducting plate

F_{g}= 6.67 10⁻¹¹ 1.67 10⁻²⁷ 9.1 10⁻³¹ / (0.5 10⁻³)²

F_{g} = 4.1 10⁻⁵¹ N

electric force

F_{e} = -e E

F_{e} = - 1.6 10⁻¹⁹ 145.6

F_{e} = 2.3 10⁻¹⁷ N

let's look for the reason between these two forces

F_{e} / F_{g} = 2.3 10⁻¹⁷ / 4.1 10⁻⁵¹

F_{e} /F_{g} = 10³⁴

We see that the electric force is many orders of magnitude higher than the gravitational force.