Question

HELP

If a certain cannon is fired from a height of 8.4 meters above the ground, at a certain angle, the height of the cannonball above the ground, h,

in meters, at time, t, in seconds, is found by the function h(t) = -4.91? + 30.5t + 8.4. Find the time it takes for the cannonball to strike the

ground.

Answer 1

The time it takes for the cannonball to hit the ground is 6.49 seconds.

Explanation:

You know that the height of the cannonball above the ground, h, in meters, in time, t, in seconds, is found by the function h(t) = -4.9t² + 30.5t + 8.4. You want to calculate the time it takes for the cannonball to hit the ground, that is, the time it takes for the bullet to reach zero height. So, being h(t) = 0 you have:

0 = -4.9t² + 30.5t + 8.4

To solve a quadratic function 0=a*x² + b*x +c, the expression is applied:

`\frac{-b+-\sqrt{b^(2) -4*a*c} }{2*a}`

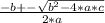
In this case, being a = -4.9, b =30.5 and c =8.4 you have:

`\frac{-30.5+-\sqrt{30.5^(2) -4*(-4.9)*8.4} }{2*(-4.9)}`

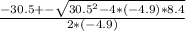
Solving you get:

t1= -0.26 seconds and t2=6.49 seconds

Since time does not have a negative value, then the time it takes for the cannonball to hit the ground is 6.49 seconds.