Answer:
the probability that exact three would be replaced under each warranty is 0.34
Explanation:
The computation of the probability that exact three would be replaced under each warranty is as follows
Given that
Submitted under warranty = P = 20%
Replaced with the new units = 40%
So replaced and submitted would be
= 40% × 20%
= 80%
Now let us assume the number of telephones be x for ending up for replacement
Total number of telephones purchased is 10
Now the probability by applying the formula of binomial probability is

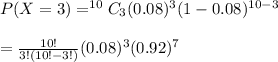
= 0.34
Hence, the probability that exact three would be replaced under each warranty is 0.34